Research Focus On Dr. Ulf D. Schiller

Fang Wang and Ulf D. Schiller, MADE in SC Thrust 3 (Interactive Biomaterials)
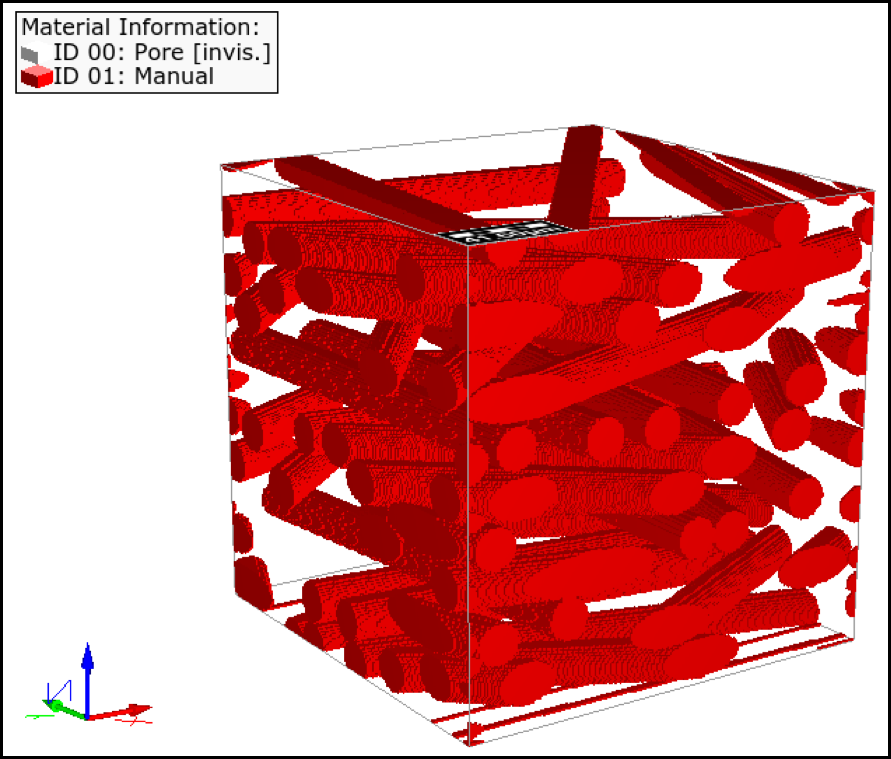
Many materials are porous media that contain pores within a skeletal matrix. Porous materials are important for a range of engineering applications, ranging from fabrics for your clothing to ceramic electrodes for batteries. The internal structure of porous materials is similar to a sponge, and the flow of fluids in porous media is a very complex phenomenon that cannot be as easily described as the flow through a pipe. Depending on the affinity between the fluid and the surfaces of the porous matrix, some fluids will flow through the material more easily than others. This concept is used applications such as filtration. For example, to sequester water droplets from diesel fuel, a coalescing filter is used that consists of porous membranes made from small fibers. When the mixture flows through the filter, water droplets collect on the fibers and merge into larger and larger droplets (coalescence) that are eventually pulled into the sump area by gravity. The efficiency of this process has a significant impact on the performance and lifetime of diesel engines. The geometric structure and surface properties of the filter material have a complicated influence on the filtration efficiency. The Schiller Research Group at Clemson University develops computational models and performs computer simulations of flow through porous media to investigate the relationship between the microscopic pore structure and the macroscopic transport properties. An example of a three-dimensional fibrous geometry is shown in Figure 1. The computer simulations can be used to optimize the porous materials and to design more efficient filtration devices while reducing the development costs.
In a first step towards understanding the filtration of droplets in fibrous media, we have studied the wetting behavior of a single droplet on two parallel fibers. Figure 2 shows the evolution of a droplet that initially has a spherical shape and then spreads along the fibers. The final shape of the droplet depends on the volume of the droplet, the size of the fibers, the distance between the fibers, and the surface properties (wettability) of the fibers. As one would expect, water droplets spread out more on a surface that has an affinity to water (hydrophilic) than on a surface that repels water (hydrophobic, similar to Teflon). We have observed three possible equilibrium configurations in our simulations: barrel-shaped droplets, droplet bridges, and long columns. Interestingly, the transitions between the droplet shape and the column shape occur at different points depending on where we start. This behavior is called hysteresis and could be exploited to capture droplets in complex fibrous media. We have developed a theoretical model to describe the droplet configuration that allows us to calculate the critical drop volume and fiber distance of the shape transition. Our simulation data agree well with the theoretical predictions and with experimental measurements. Our model thus settles the question of hysteresis behavior of the shape transitions observed in experiments and offers new insights into the spreading of droplets on fibers. In the next stage, we will study droplets in more complex fiber arrangements and in realistic porous geometries. This will show us how we can influence the liquid distribution during coalescence filtration by changing the geometric structure and surface properties of the porous materials. We also plan to simulate the multicomponent flow through fibrous filters under processing conditions.
September 18, 2019